0x00 기초 정렬
정렬의 종류는 약 30개로 매우 많다. 여기서는 모든 정렬 알고리즘을 다 다루지는 않을거고 대표적인 몇 개만 다룰것이다.
크기순으로 정렬하려고 한다면 다음과 같이 생각해서 정렬할 수 있을것이다.
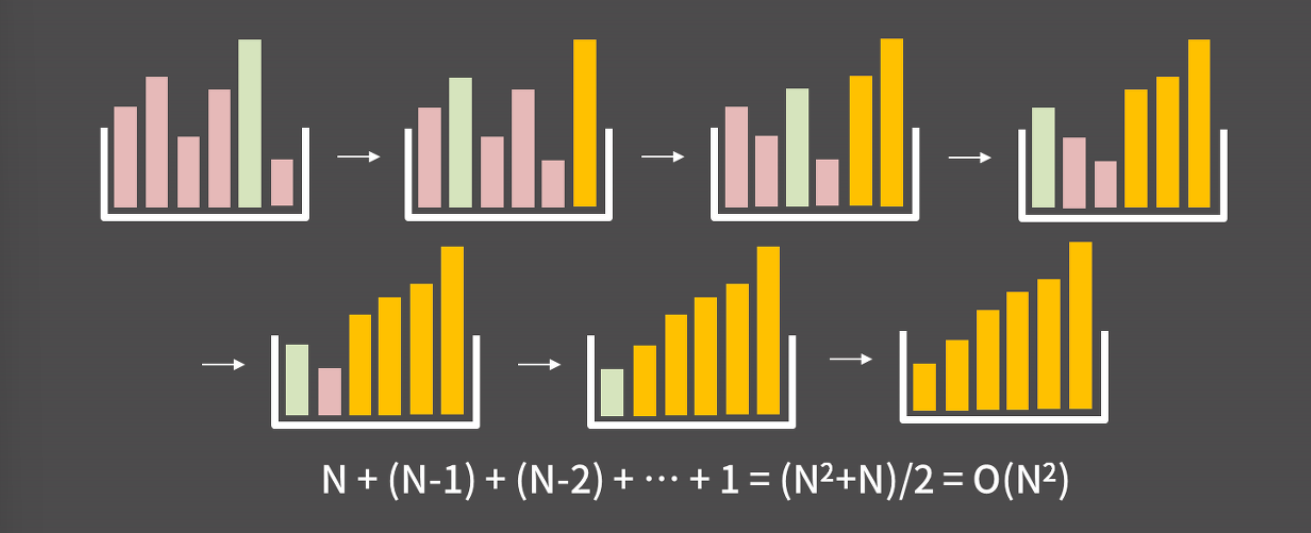
선택 정렬

버블 정렬
앞에서부터 인접한 두 원소를 보면서 앞의 원소가 뒤의 원소보다 클 경우 자리를 바꾸는 것을 반복하면 자연스럽게 제일 큰 것부터 오른쪽에 쌓이게 된다.



위에서 소개된 선택 정렬과 버블 정렬 외에 삽입 정렬이라는 것도 있는데 이들은 모두 O(N^2)에 동작하는 대표적인 정렬 방법이다. 하지만 N이 커질수록 이 방법들은 비효율적일 것이다. 그래서 정렬을 더 빠르게 수행할 수 있는 알고리즘들을 알아보겠다.
0x01 Merge Sort
Merge Sort는 재귀적으로 수열을 나눠 정렬한 후 합치는 정렬법이다. 이 알고리즘은 시간복잡도가 O(NlgN)에 동작한다.
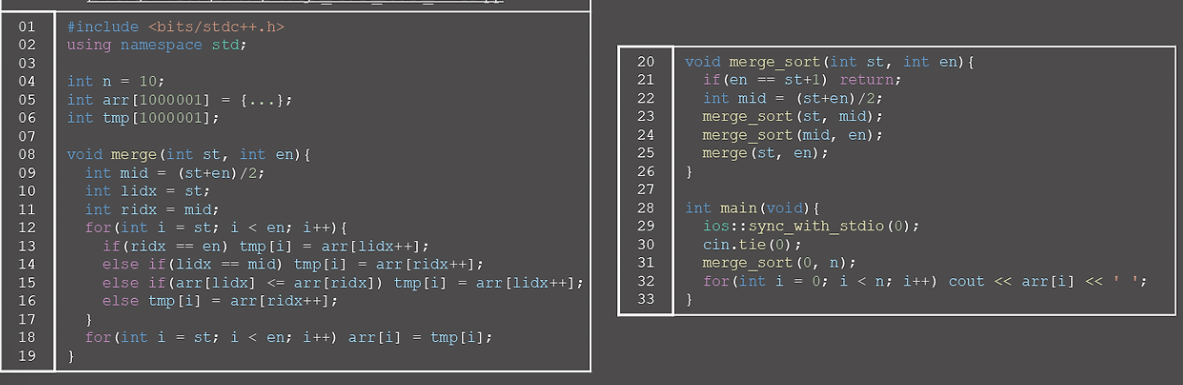
배열 합치기
우선 길이가 N, M인 두 정렬된 리스트를 합쳐서 길이 N+M의 정렬된 리스트를 만드는 방법을 알아보자.



11728번: 배열 합치기
첫째 줄에 배열 A의 크기 N, 배열 B의 크기 M이 주어진다. (1 ≤ N, M ≤ 1,000,000) 둘째 줄에는 배열 A의 내용이, 셋째 줄에는 배열 B의 내용이 주어진다. 배열에 들어있는 수는 절댓값이 109보다 작거
www.acmicpc.net
#include <bits/stdc++.h>
using namespace std;
int n, m;
int a[1000005], b[1000005], c[2000010];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
int n, m;
cin >> n >> m;
for(int i = 0; i < n; i++) cin >> a[i];
for(int i = 0; i < m; i++) cin >> b[i];
int aidx =0, bidx = 0;
for(int i =0; i < n+m; i++) {
if(aidx == n) c[i] = b[bidx++];
else if(bidx == m) c[i] = a[aidx++];
else if(a[aidx] <= b[bidx]) c[i] = a[aidx++];
else c[i] = b[bidx++];
}
for(int i=0; i<n+m; i++) cout << c[i] << ' ';
}
Merge Sort
Merge Sort는 3단계로 요약이 가능하다
- 주어진 리스트를 2개로 나눈다
- 나눈 리스트 2개를 정렬한다
- 정렬된 두 리스트를 합친다
나눈 리스트를 어떻게 정렬할것이냐는 재귀를 이용하면 된다. 예를 들어 길이가 8인 리스트를 정렬하려면 길이가 4인 리스트를 정렬할 수 있어야 하고, 길이가 4인 리스트를 정렬하려면 길이가 2인 리스트를 정렬할 수 있어야 하며 이는길이가 1인 리스트도 정렬할 수 있어야 되는데 길이가 1인 리스트는 바로 정렬이 되므로 결국 길이가 8인 리스트도 정렬 가능하다는 것이다.
길이는 N = 2^k


Stable Sort
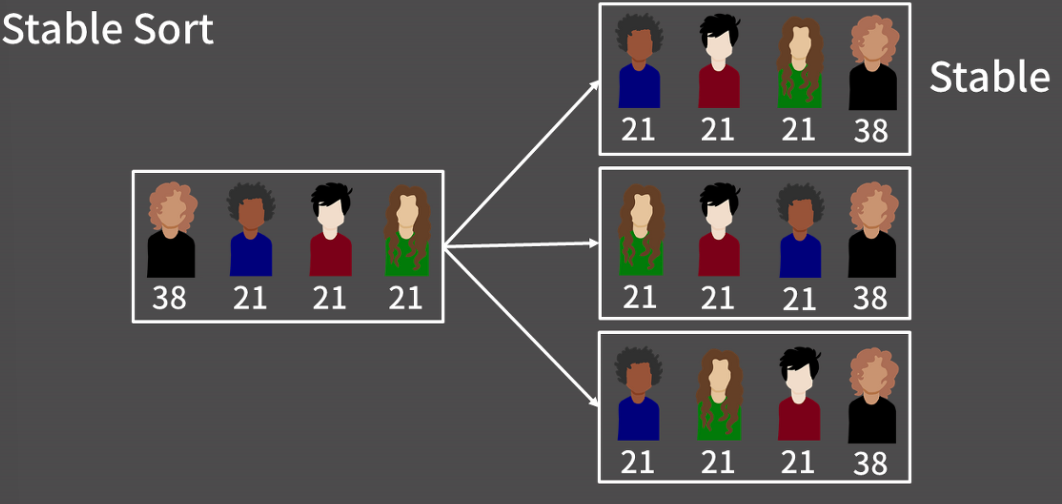
지금 이 사람들을 나이 순으로 정렬하는 상황을 생각해보자. 편의상 상의 색깔로 사람을 지칭하면 지금 파랑, 빨강, 초록은 나이가 21살로 다 똑같고 검정만 혼자 38살이다. 그래서 나이 순으로 정렬을 한다치면 오른쪽 세 가지가 모두 올바른 정렬이다. 이렇게 우선 순위가 강ㅌ은 원소가 여러 개일 땐 정렬한 결과가 유일하지 않을 수 있다. 이때, 우선 순위가 같은 원소들끼리는 원래의 순서를 따라가도록 하는 정렬이 Stable Sort이다.
여러 정렬이 가능한 것을 Unstable Sort라 한다. Merge Sort는 Stable Sort이다.
0x02 Quick Sort
Quick Sort는 거의 모든 정렬 알고리즘 보다 빨라서 각종 라이브러리의 정렬은 대부분 퀵 소트를 바탕으로 만들어져 있다. 주의해야 할 점은 코딩테스트에서 STL을 못 쓰고 직접 정렬을 구현해야 한다면 절대로! 퀵 소트를 쓰지 말고 Merge Sort나 힙 소트, 다른 O(NlgN) 정렬을 사용해야 한다.
Quick Sort도 머지 소트처럼 재귀적으로 구현되는 정렬이다. 퀵 소트에서는 매 단계마다 pivot이라고 이름 붙은 원소 하나를 제자리로 보내는 작업을 반복한다. 그렇다면 pivot을 어떻게 제자리로 보낼까?
예를 들어 다음과 같은 배열이 있다고 해보자. 6이 pivot이고 l은 pivot보다 큰 값이 나올 때 까지 오른쪽으로 이동하고 r은 pivot보다 작거나 같은 값이 나올 때 까지 왼쪽으로 이동한다. 그 다음 두 포인터가 가리키는 원소의 값을 스왑한다. 이걸 l과 r이 교차할 때 까지 반복한다.



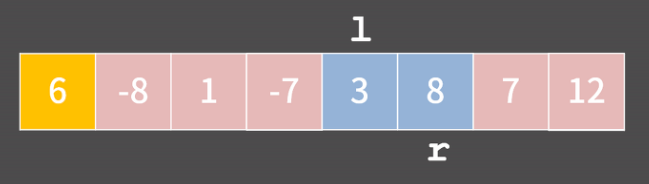
위 과정을 반복하다 보니 l과 r이 교차하는 순간이 발생한다. 이렇게 r이 l보다 작아진 순간이 오면 pivot과 r을 스왑하면서 알고리즘이 끝나게 된다.



결과를 보면 pivot 왼쪽에는 3, -8, 1, -7 이 있고 오른쪽에는 8, 7, 12가 됐으니 제자리를 잘 찾아갔다. 왜 이렇게 됬냐면은 모든 순간에 l의 왼쪽에는 pivot보다 작거나 같은 원소들만 있고 r의 오른쪽에는 pivot보다 큰 원소들만 있다는 점에 주목하면 된다. 이걸 재귀적으로 만들면 Quick Sort가 완성된다. base conditon은 현재 보는 구간의 길이가 1 이하일 때이고 pivot을 제자리로 보낸 뒤 재귀적으로 자기 자신을 호출하게 하면 된다.
#include <bits/stdc++.h>
using namespace std;
int n = 10;
int arr[1000001] = {15, 25, 22, 357, 16, 23, -53, 12, 46, 3};
void quick_sort(int st, int en) { // arr[st to en-1]을 정렬할 예정
if(en <= st+1) return; // 수열의 길이가 1 이하이면 함수 종료.(base condition)
int pivot = arr[st]; // 제일 앞의 것을 pivot으로 잡는다. 임의의 값을 잡고 arr[st]와 swap해도 상관없음.
int l = st+1; // 포인터 l
int r = en-1; // 포인터 r
while(1){
while(l <= r && arr[l] <= pivot) l++;
while(l <= r && arr[r] >= pivot) r--;
if(l > r) break; // l과 r이 역전되는 그 즉시 탈출
swap(arr[l], arr[r]);
}
swap(arr[st], arr[r]);
quick_sort(st, r);
quick_sort(r+1, en);
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
quick_sort(0, n);
for(int i = 0; i < n; i++) cout << arr[i] << ' ';
}
장점
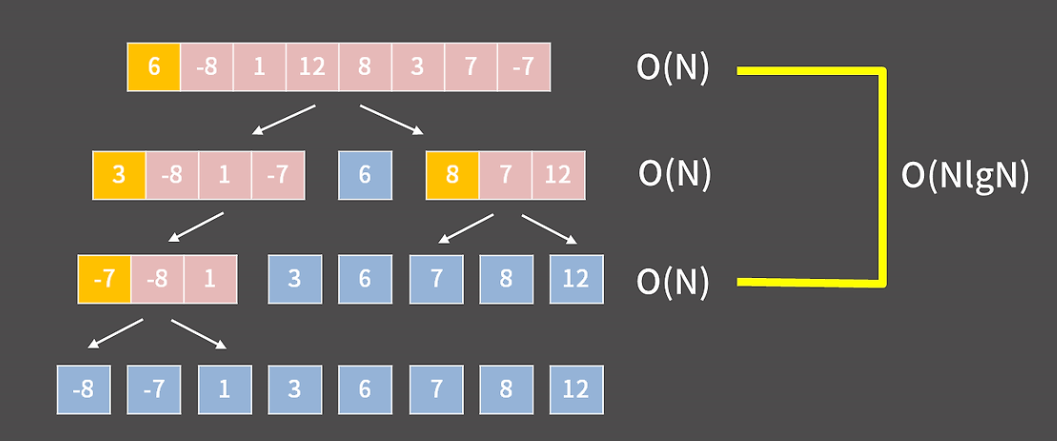
퀵 소트의 장점은 추가적인 공간이 필요하지 않다는 점이다. 또 그렇게 그 배열 안에서의 자리 바꿈만으로 처리가 되기 때문에 cache hit rate가 높아서 속도가 빠르다는 장점도 따라온다. 이렇게 추가적인 공간을 사용하지 않는 정렬을 In-Place Sort라고 부른다.
퀵 소트의 과정을 풀이해보면 위 사진과 같다. 맨 처음 pivot은 6으로 제자리를 찾아가면 6을 기준으로 양쪽이 나뉘게 된다. 양쪽에서 각각 pivot을 제자리로 보내고, 이 과정을 계속 반복한다. 각 단계마다 O(N)이 필요할 것이고 매번 완벽하게 중앙에 위치해서 리스트를 균등하게 둘로 쪼갠다면 단계의 개수는 lgN이 될거고 전체적으로는 O(NlgN)이다. 평균적으로는 이렇다.
단점

그런데 퀵 소트에는 치명적인 단점이 있다. 1,2,3,4,5,6,7,8을 퀵 소트로 정렬하면 시간복잡도가 얼마일까?
매번 선택되는 pivot은 중앙에 가는 대신 제일 왼쪽에 위치하게 되고 그로 인해 단계는 lgN개가 아닌 N개가 된다. 그리고 시간복잡도를 계산하면 O(N^2)이다. 이 경우에서볼 수 있듯이 퀵 소트는 평균적으로 O(NlgN)이지만 최악의 경우 O(N^2)이다. 단순히 제일 왼쪽의 값을 pivot으로 선택해보면 지금처럼 리스트가 오름차순이거나 내림차순일 때에 바로 O(N^2)된다.
STL이 없을 때 정렬을 짜야 한다면 퀵 소트를 절대 쓰지 말라는 이유가 바로 이것이다. Merge Sort가 Quick Sort보다 느린건 맞지만 어차피 O(NlgN)에 돌아가니 충분히 빠르다. 최악의 경우를 가진 Quick Sort를 쓸 필요가 없다.
참고로 라이브러리에서 대부분 퀵 소트를 사용하긴 한다. 하지만 처리를 다르게 했는데 피벗을 랜덤하게 택할 수도 있고, 피벗 후보를 3개 정해서 중앙값을 피벗으로 두거나 최악의 경우에도 O(NlgN)을 보장하기 위해 Heap Sort로 정렬한다. 이러한 정렬을 Introspective Sort 라고 부른다.
정리

'공부 일지 > 알고리즘' 카테고리의 다른 글
| [바킹독 알고리즘] 0x0F - 정렬 II (0) | 2024.03.20 |
|---|---|
| [바킹독 알고리즘] 0x19강 - 트리 (0) | 2024.02.26 |
| [바킹독 알고리즘] 0x18강 - 그래프 (0) | 2024.02.23 |
| [바킹독 알고리즘] 0x16강 - 이진 검색 트리 (0) | 2024.02.22 |
| [바킹독의 알고리즘] 0x0C강 - 백트래킹 (1) | 2024.01.08 |
