0x00 정의와 성질

트리 : 무방향이면서 사이클이 없는 연결 그래프(Undirected Acyclic Connected Graph)



0x01 BFS, DFS
BFS

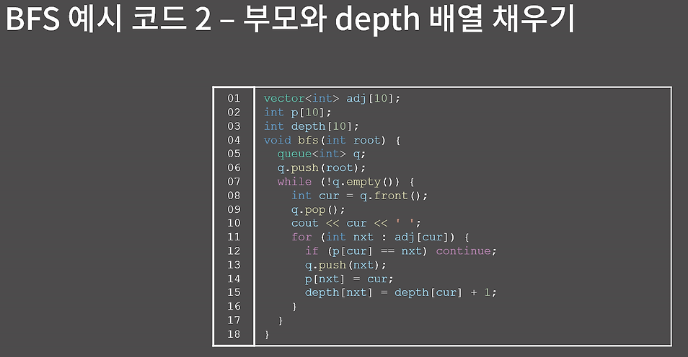
DFS



0x02 이진 트리의 순회
레벨 순회

레벨순회는 BFS랑 같다고 보면 된다. 위에서부터 흝고 내려가는 순서이다. 위 예시 순서로는 1>2>3>4>5>6>7>8 이다.
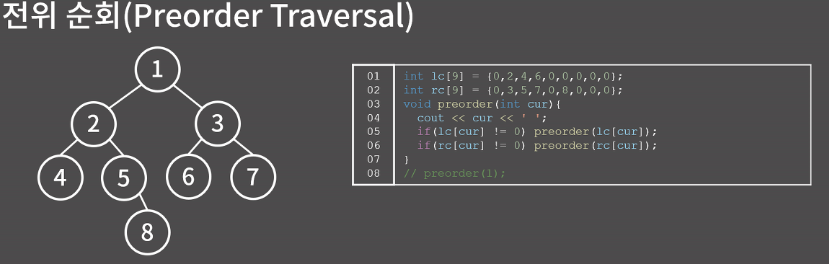
전위 순회
순서
- 현재 정점을 방문한다.
- 왼쪽 서브 트리를 전위 순회한다.
- 오른쪽 서브 트리를 전위순회한다.

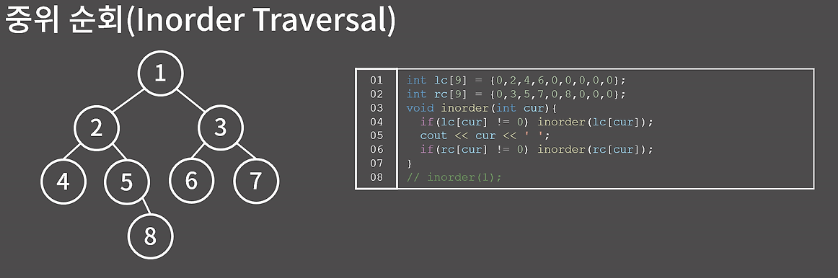
중위 순회
순서
- 왼쪽 서브 트리를 중위 순회한다.
- 현재 정점을 방문한다.
- 오른쪽 서브 트리를 중위 순회한다.
중위 순회는 왼쪽 서브트리 > 나 > 오른쪽 서브트리 순으로 처리하는 순회 방법이다.


후위 순회
순서
- 왼쪽 서브 트리를 후위 순회한다.
- 오른쪽 서브 트리를 후위 순회한다.
- 현재 정점을 방문한다.


0x03 연습 문제
BOJ 11725번:트리의 부모 찾기
11725번: 트리의 부모 찾기
루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.
www.acmicpc.net
#include <bits/stdc++.h>
using namespace std;
int n;
vector<int> adj[100005];
int p[100005];
void dfs(int cur){
for(int nxt : adj[cur]) {
if(p[cur] == nxt) continue;
p[nxt] = cur;
dfs(nxt);
}
}
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for(int i =0; i < n-1; i++){
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1);
for(int i=2; i<=n; i++) cout << p[i] << '\n';
}
BOJ 1991번: 트리 순회
1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파
www.acmicpc.net
#include <bits/stdc++.h>
using namespace std;
int n;
int lc[29];
int rc[29];
void preorder(int cur){
cout << char(cur+'A'-1);
if(lc[cur] != 0) preorder(lc[cur]);
if(rc[cur] != 0) preorder(rc[cur]);
}
void inorder(int cur){
if(lc[cur] != 0) inorder(lc[cur]);
cout << char(cur+'A'-1);
if(rc[cur] != 0) inorder(rc[cur]);
}
void postorder(int cur){
if(lc[cur] != 0) postorder(lc[cur]);
if(rc[cur] != 0) postorder(rc[cur]);
cout << char(cur+'A'-1);
}
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for(int i=1; i<=n; i++){
char c, l, r;
cin >> c >> l >> r;
if(l != '.') lc[c-'A'+1] = l-'A'+1;
if(r != '.') rc[c-'A'+1] = r-'A'+1;
}
preorder(1); cout << '\n';
inorder(1); cout << '\n';
postorder(1); cout << '\n';
}
'공부 일지 > 알고리즘' 카테고리의 다른 글
| [바킹독 알고리즘] 0x0F - 정렬 II (0) | 2024.03.20 |
|---|---|
| [바킹독 알고리즘] 0x0E강 - 정렬 I (0) | 2024.03.10 |
| [바킹독 알고리즘] 0x18강 - 그래프 (0) | 2024.02.23 |
| [바킹독 알고리즘] 0x16강 - 이진 검색 트리 (0) | 2024.02.22 |
| [바킹독의 알고리즘] 0x0C강 - 백트래킹 (1) | 2024.01.08 |
