0x00 정의와 표현법
정의
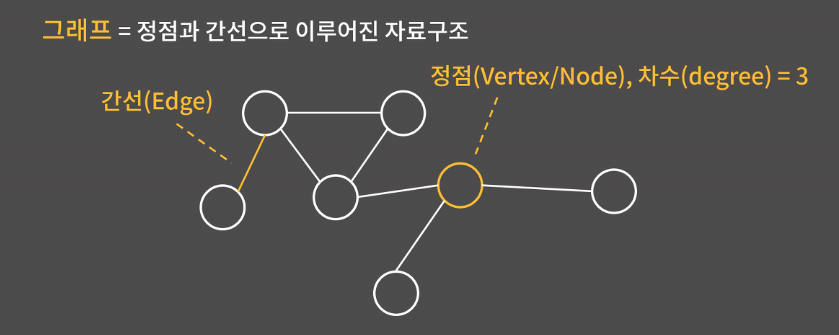
그래프란 정점과 간선으로 이루어진 자료구조를 말한다. 차수는 각 정점에 대해서 간선으로 연결된 이웃한 정점의 개수이다. 그래프는 네비게이션에서 최단 경로 찾기, 혹은 구글 같은 검색엔진에서 랭킹 정하기와 같이 뭔가 원소 사이의 연결 관계를 설정해야 하는 상황에서 유용하게 활용될 수 있는 자료구조이다.
간선
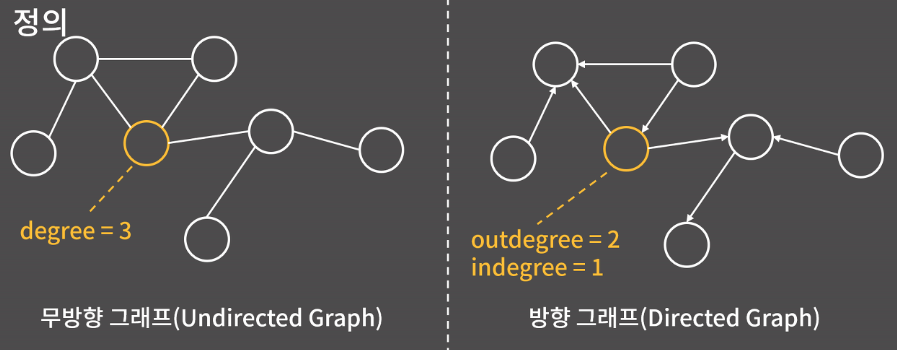
그래프의 간선에는 방향성이 있을 수 있다. 왼쪽처럼 방향성이 없다면 무방향 그래프라고 하고 방향성이 있다면 방향 그래프라고 한다. 간선에 방향성이 있다는건 마치 일방통행 도로를 생각하면 된다.
방향 그래프에서도 차수라는 개념이 있는데 자기에게서 나가는 간선의 개수는 outdegree(차출 차수)이고 들어오는 개수는 indegree(진입 차수)이다.
그래프의 종류

사이클이란 임의의 한 점에서 출발해 자기 자신으로 돌아올 수 있는 경로를 말한다. 그래프 안에 사이클이 하나라도 있으면 순환 그래프(Cyclic graph)라고 하고 사이클이 하나도 없으면 비순환 그래프(Acyclic graph)라고 한다. 그래프가 방향 그래프인지 무방향 그래프인지 무관하게 동일하다. 오른쪽의 경우에는 얼핏 보면 왼쪽처럼 사이클이 있는 것처럼 보이지만 간선의 방향성으로 인해 사이클이 없다는 거에 유의하자.
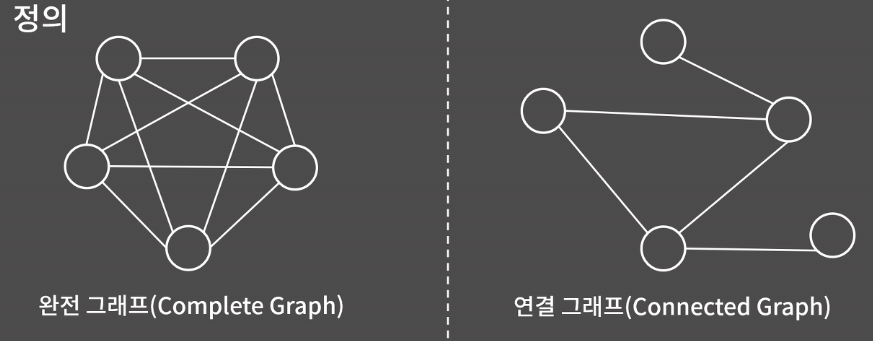
또한 모든 서로 다른 정점이 쌍이 간선으로 연결된 그래프를 완전 그래프(Complete Graph)라고 부른다. 그리고 임의의 두 정점 사이에 경로가 항상 존재하는 그래프는 연결 그래프(Connected Graph)라고 부른다.

그래프는 꼭 연결되어 있을 필요도 없고, 두 정점 사잉의 간선이 반드시 1개 이하일 필요도, 또 간선이 반드시 서로 다른 두 정점을 연결해야 할 필요도 없다. 또, 오른쪽 그림처럼 한 정점에서 시작해 같은 정점으로 들어오는 간선이 있을 수도 있다. 이런 간선을 루프(loop)라고 부른다.
보통 문제에서는 필요에 따라 "그래프는 연결되어 있다/그래프는 연결그래프이다", "두 정점 사이의 간선은 최대 1개 존재한다/같은 간선은 한 번만 주어진다", "간선의 두 정점은 서로 다르다/간선은 서로 다른 두 정점을 연결한다"와 같이 조건을 엄밀하게 지정하는 경우가 많다. 그러나 이러 추가적인 조건이 주어지지 않았다면 그림에 있는 그래프처럼 그래프가 분리되어 있거나, 같은 간선이 여러 개 있거나, 혹은 루프가 있거나 하는 형태에 대해서도 올바른 답을 낼 수 있게 코드를 짜야한다는걸 기억해야 한다. 참고로 두 정점 사이의 간선이 1개 이하이고 루프가 존재하지 않는 그래프를 우리는 단순 그래프(Simple Graph)라고 한다.
표현법
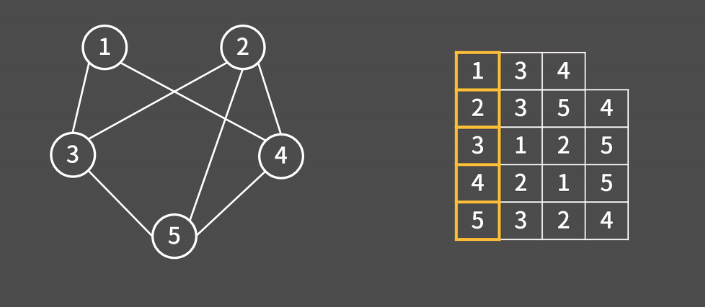
표현법 1 - 인접 행렬
인접 행렬로 그래프를 나타내면 정점이 V개이고 간선이 E개일 때 어떤 두 점이 연결되어 있는지를 O(1)에 알 수 있다는 장점이 있다. 그리고 가로와 세로가 각각 V인 2차원 배열이 필요하니 O(pow(V,2))의 공간을 필요로 한다. 또 어떤 점에 연결되어 있는 모든 정점의 목록을 알아내고 싶을 때에도 개수와 무관하게 시간복잡도가 O(V)이다.
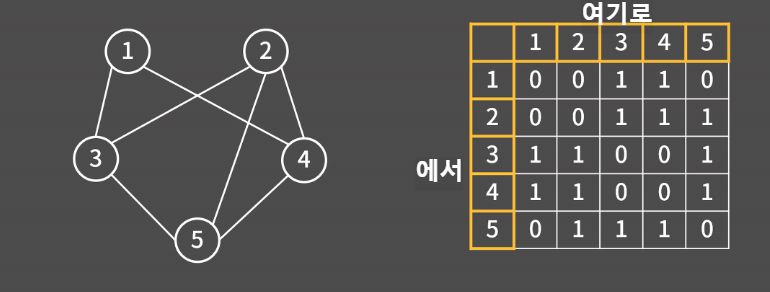

만약 단순 그래프가 아니라고 한다면 1 or 0으로만 나타내지 말고 간선이 3개이면 3을 쓰고, 4개이면 4를 쓰는 식으로 변형을 하면 된다.

먼저 방향 그래프의 예시를 보면 adj_matrix 배열을 선언한 후에 간선을 입력 받으면서 adj_matrix[u][v] = 1로 만들면 끝이다. 만약 이게 무방향 그래프였다면 adj_matrix[u][v]와 adj_matrix[v][u]를 모두 1로 만들면 된다. 여기까지가 행렬을 이용하는 방법이다.
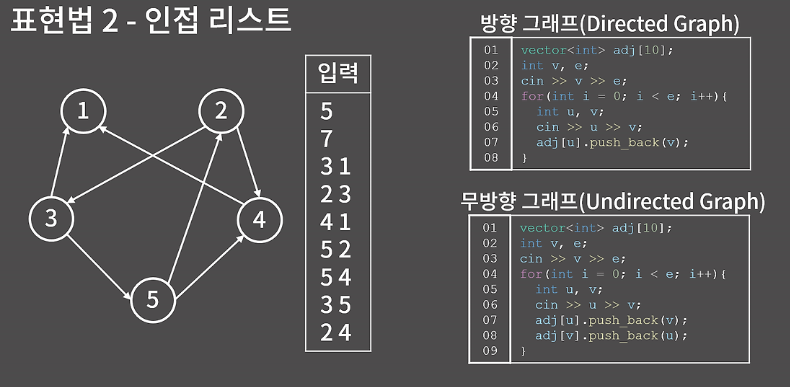
표현법 2 - 인접 리스트
이 방식은 인접 행렬과 비교했을 때 정점이 더 많고 간선은 상대적으로 적은 상황에서 공간을 절약할 수 있는 방식이다. 경우에 따라 인접행렬로는 절대 저장이 불가능해 인접 리스트를 써야만하는 상황이 종종 있다.
V개의 리스트를 만들어 각 리스트에 자신과 연결된 정점을 넣으면 끝이다.

인접 행렬에서는 V by V 크기의 배열을 선언했어야 하니 O(pow(V,2))의 공간이 필요했는데 인접 리스트에서는 O(V+E)의 공간이 필요하다. 일단 리스트가 V개 필요하고, 리스트에서 원소의 개수의 총합은 E개, 무방향 그래프일 때 2E개이기 때문이다.
만약 STL을 안쓰고 구현을 해야 한다면?


정리

BFS, DFS나 여러 경로 알고리즘들에서는 전부 특정 정점에 연결된 모든 정점을 확인하는 작업이 반복적으로 등장하게된다. 그렇기 때문에 앞으로 인접 행렬 보다는 인접 리스트로 그래프를 나타낼 상황이 훨씬 많다.
0x01 BFS



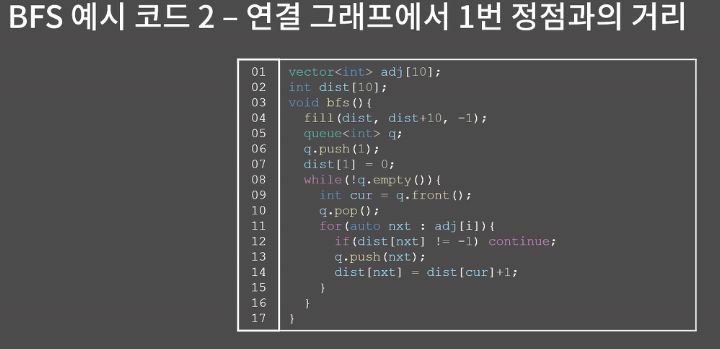
BFS 단원에서 응용을 소개할 때 다룬 내용이지만 그래프에서도 시작점에서 다른 모든 점으로의 최단 경로를 찾을 때 BFS를 이용할 수 있다. BFS의 과정 중에서 현재 보는 정점으로부터 추가되는 인접한 정점은 시작점으로부터 1만큼 더 떨어져 있다. 즉 모든 간선의 길이가 동일한 상황에서 두 지점 사이의 거리를 찾는 문제는 BFS로 해결이 가능하다. 하지만 만약 모든 간선의 길이가 다르다면 이 문제는 플로이드나 다익스트라와 같은 다른 알고리즘을 사용해야된다.


0x02 DFS
BFS과정에서 큐만 스택으로 바꾸면 DFS 과정이 된다.





0x03 연습문제
BOJ 11724번: 연결 요소의 개수
11724번: 연결 요소의 개수
첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 같은 간선은 한 번만 주어
www.acmicpc.net
#include <bits/stdc++.h>
using namespace std;
vector<int> nd[1005];
bool vis[1005];
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
int n, m;
//그래프 리스트 만들기
cin >> n >> m;
while(m--){
int u, v;
cin >> u >> v;
nd[u].push_back(v);
nd[v].push_back(u);
}
//BFS시작
int num = 0;
for(int i = 1; i <= n; i++){
if(vis[i]) continue;
num++;
queue<int> q;
q.push(i);
vis[i] = true;
while(!q.empty()){
int cur = q.front();
q.pop();
for(auto nxt : nd[cur]){
if(vis[nxt]) continue;
q.push(nxt);
vis[nxt] = true;
}
}
}
cout << num;
}
BOJ 1260번: DFS와 BFS
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
#include <bits/stdc++.h>
using namespace std;
int n,m,st;
vector<int> adj[1001];
bool vis[1001];
// 비재귀 DFS
void dfs1(){
stack<int> s;
s.push(st);
while(!s.empty()){
int cur = s.top();
s.pop();
if(vis[cur]) continue;
vis[cur] = true;
cout << cur << ' ';
for(int i = 0; i < adj[cur].size(); i++){
// 스택의 특성상 정점을 역순으로 넣어야 함
int nxt = adj[cur][adj[cur].size()-1-i];
if(vis[nxt]) continue;
s.push(nxt);
}
}
}
// 재귀 DFS
void dfs2(int cur){
vis[cur] = true;
cout << cur << ' ';
for(auto nxt : adj[cur]){
if(vis[nxt]) continue;
dfs2(nxt);
}
}
void bfs(){
queue<int> q;
q.push(st);
vis[st] = true;
while(!q.empty()){
int cur = q.front();
cout << cur << ' ';
q.pop();
for(auto nxt : adj[cur]){
if(vis[nxt]) continue;
q.push(nxt);
vis[nxt] = true;
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m >> st;
while(m--){
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
// 번호가 작은 것 부터 방문하기 위해 정렬
for(int i = 1; i <= n; i++)
sort(adj[i].begin(), adj[i].end());
dfs1(); // dfs2(st);
cout << '\n';
fill(vis+1, vis+n+1, false);
bfs();
}
'공부 일지 > 알고리즘' 카테고리의 다른 글
| [바킹독 알고리즘] 0x0E강 - 정렬 I (0) | 2024.03.10 |
|---|---|
| [바킹독 알고리즘] 0x19강 - 트리 (0) | 2024.02.26 |
| [바킹독 알고리즘] 0x16강 - 이진 검색 트리 (0) | 2024.02.22 |
| [바킹독의 알고리즘] 0x0C강 - 백트래킹 (1) | 2024.01.08 |
| [바킹독 알고리즘]0x0B강 - 재귀 (0) | 2024.01.08 |
