[바킹독 알고리즘] 0x16강 - 이진 검색 트리

0x00 정의와 성질

 

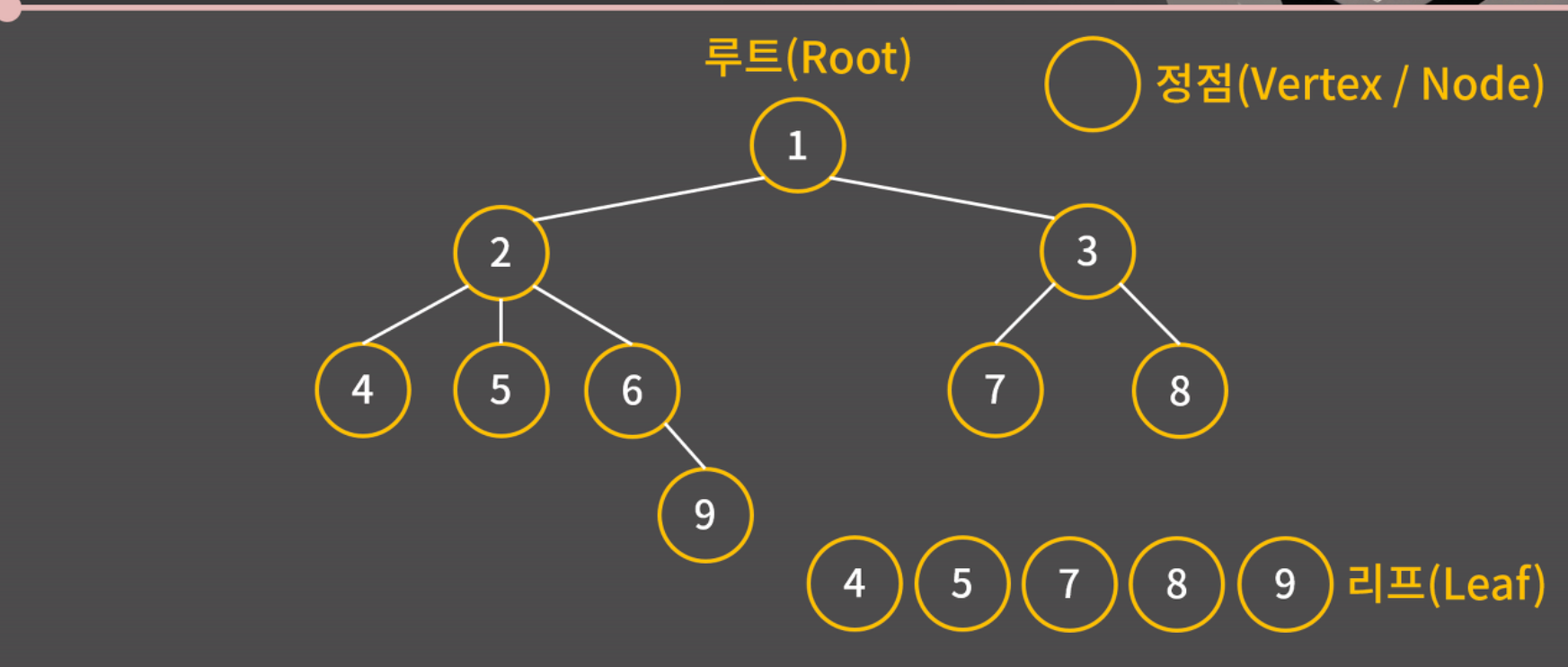
트리는 위 그림처럼 계층 구조를 가지고 있고, 제일 꼭대기를 제외하고 각 동그라미들은 위로 딱 1개와 연결되어있는 구조

 

• 각 원소는 정점 or 노드 라고 부름
• 트리의 제일 꼭대기 정점을 루트(Root)라고 부름
• 제일 말단에서 아래로 뻗은게 없는 정점을 리프(Leaf)라고 부름
• 정점과 정점을 연결하는 선을 간선이라고 부름
• 간선으로 연결된 위 아래의 관계를 부모 자식 관계라고 부름(ex.3번 정점과 7,8번 정점은 부모 자식 관계)
• 어떤 한 정점에 대해 그 밑에 있는 정점과 간선만을 모은 트리를 서브트리라고 함
• 트리의 높이는 위 아래로 뻗어있는 정도를 나타냄

 

 

이진 트리,,, 각 노드의 자식이 2개 이하인 트리를 말한다. 자식이 2개 이하이기 때문에 자식을 왼쪽 자식과 오른쪽 자식으로 구분할 수 있다.

 

 

이진 검색 트리(Binary Search Tree),,, 왼쪽 서브트리의 모든 값은 부모의 값보다 작고 오른쪽 서브트리의 모든 값은 부모의 값보다 큰 이진 트리

 

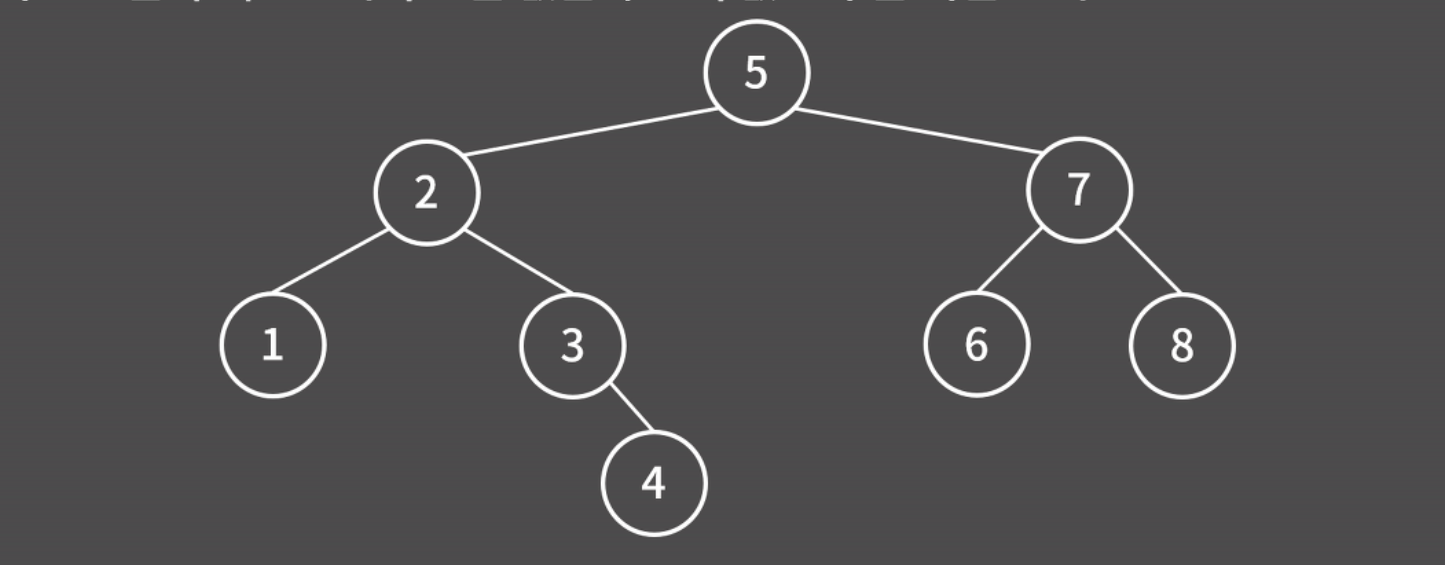
이진 검색 트리를 활용하면 insert, erase, find update 를 모두 O(lgN)에 처리할 수 있다. 또, 원소가 크기 순으로 정렬된다.

 

 

 

 

0x01 기능

Insert

완성

 

 

 

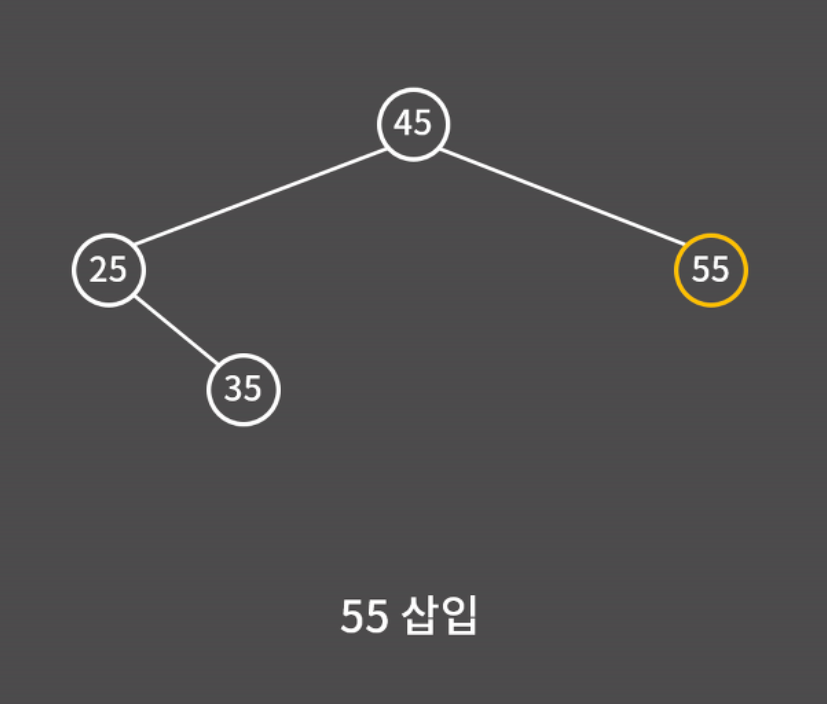
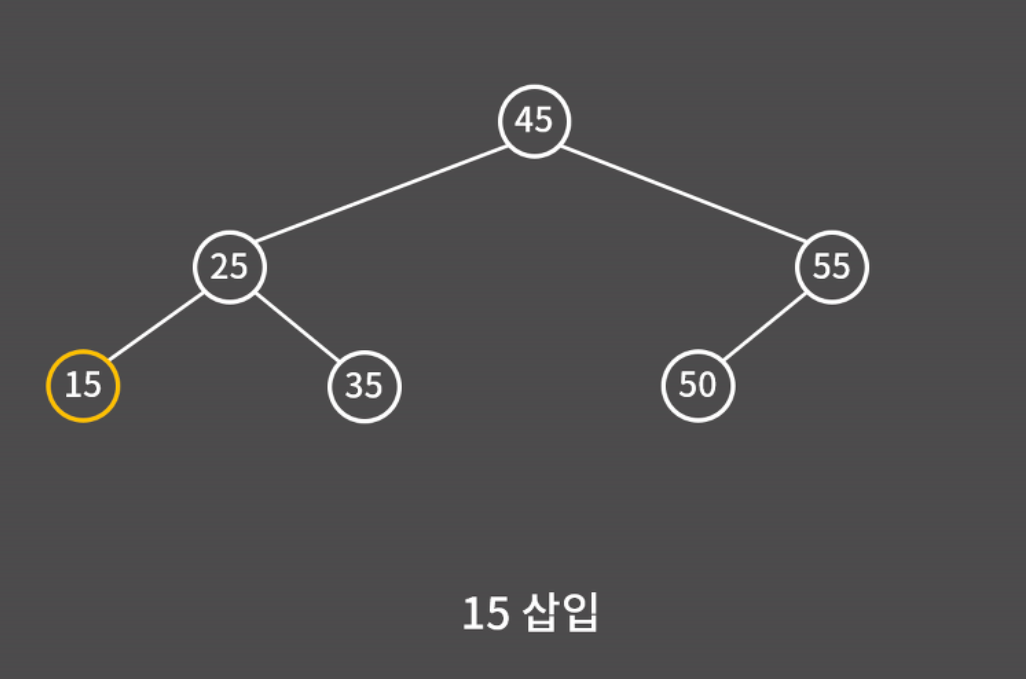
find

검색도 삽입과 비슷하게 루트에서 출발한 후 좌우로 움직이면 된다.

 

 

 

erase

무턱대고 지워버리면 트리 구조가 깨져버린다.

 

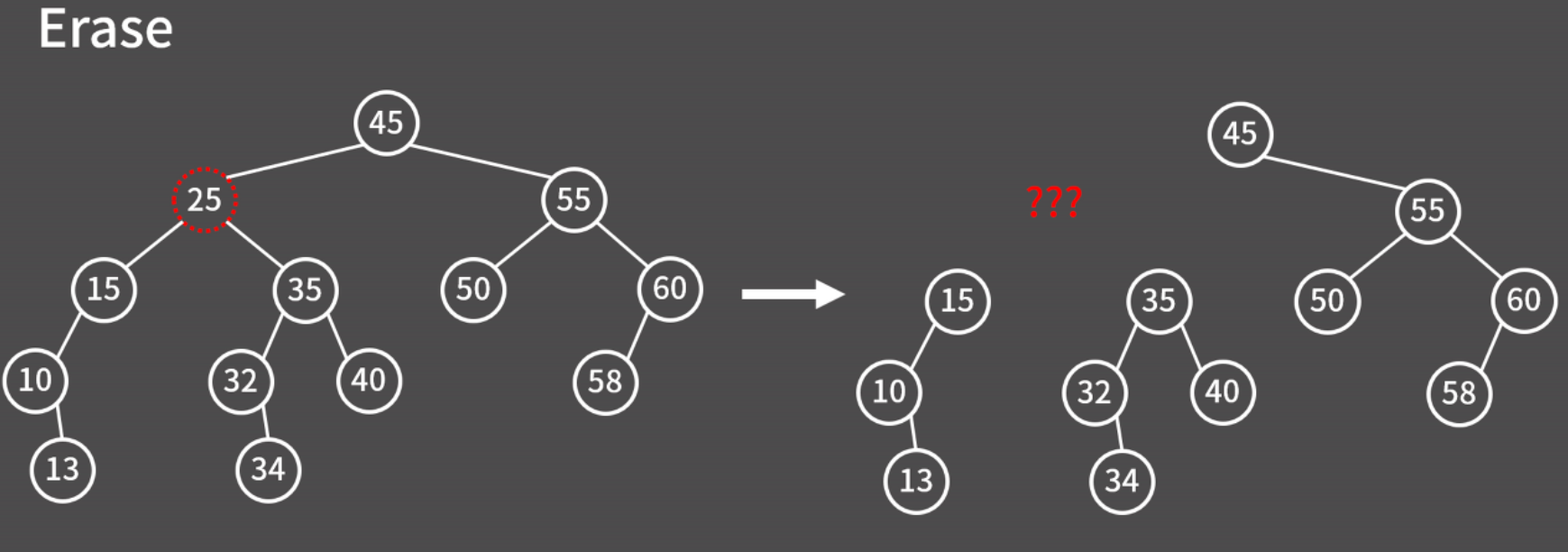
Case I, 자식이 없는 정점을 지울 때

그냥 지워도 됨

 

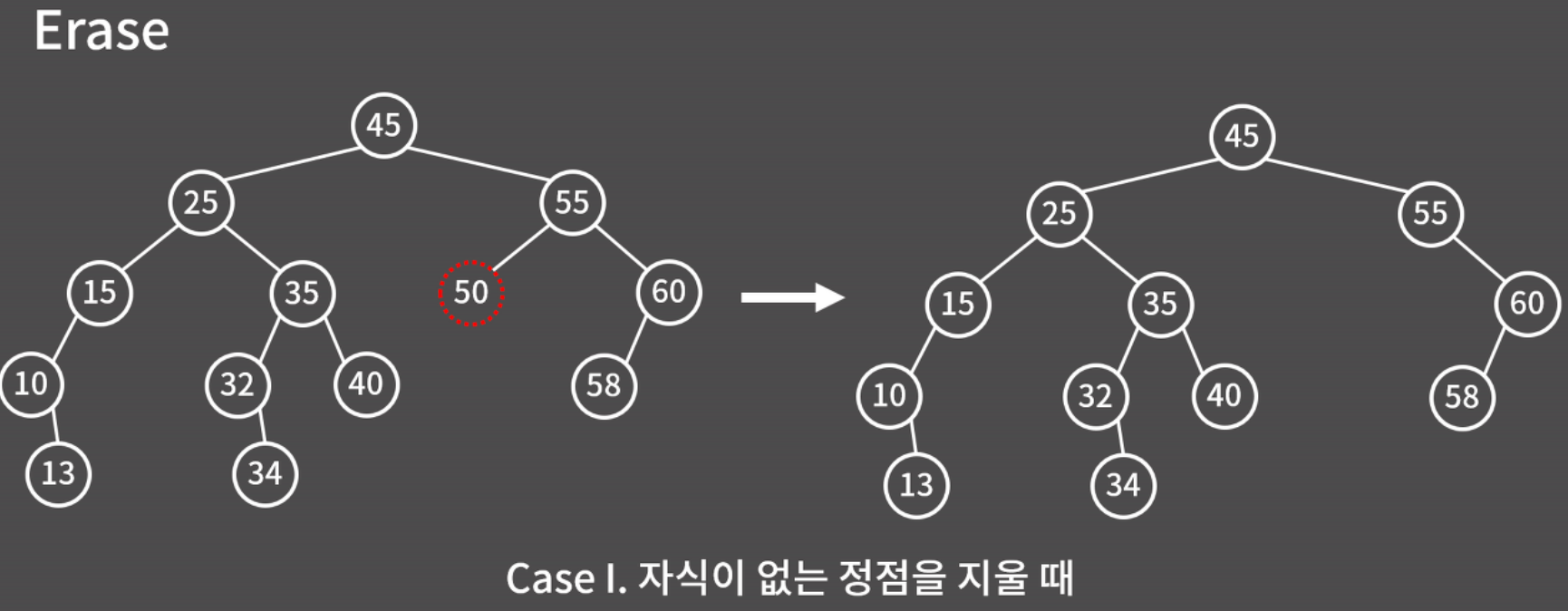
Case II, 자식이 1개인 정점을 지울 때

자식을 지워진 노드의 자리에 올리면 됨

 

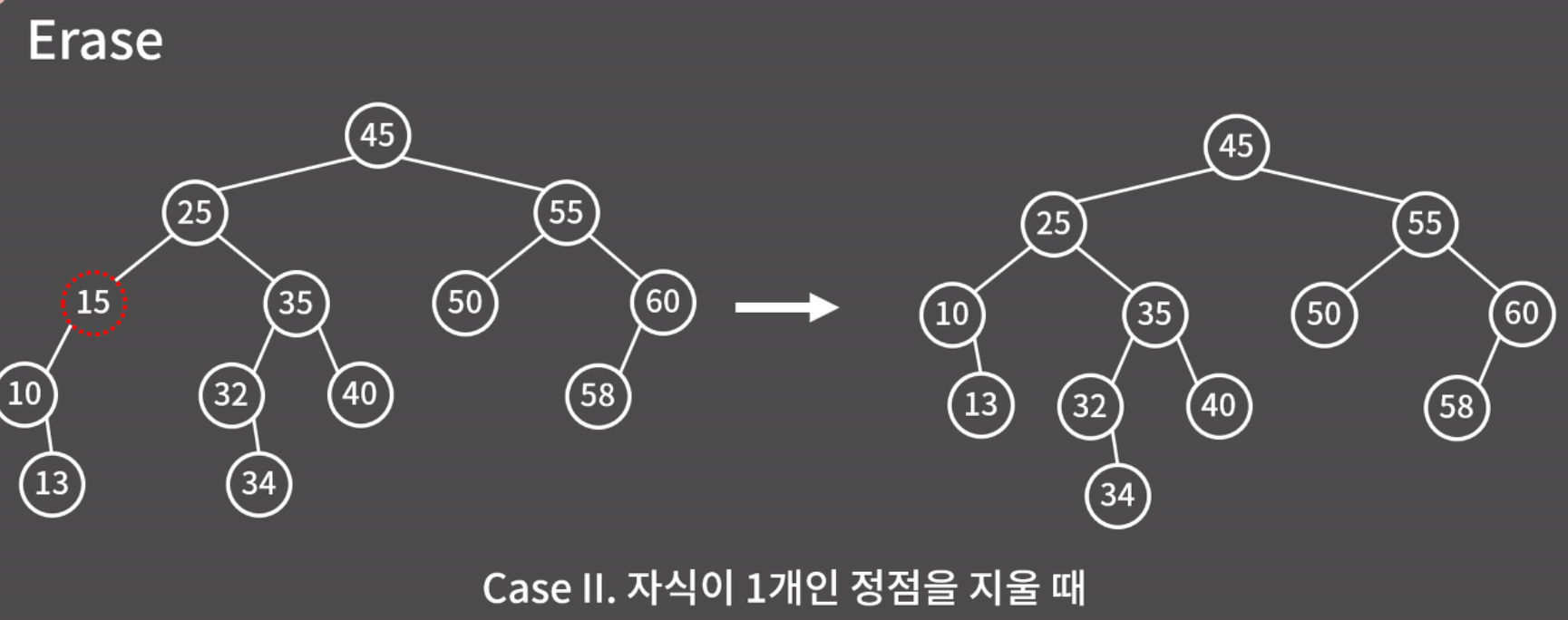
Case III, 자식이 2개인 정점을 지울 때

25보다 크면서 가장 작은 원소가 32라서 대체 가능, 지울 노드 보다 큰 수 중에서 가장 작은 자식 노드가 대체가능하다.

 

 

 

 

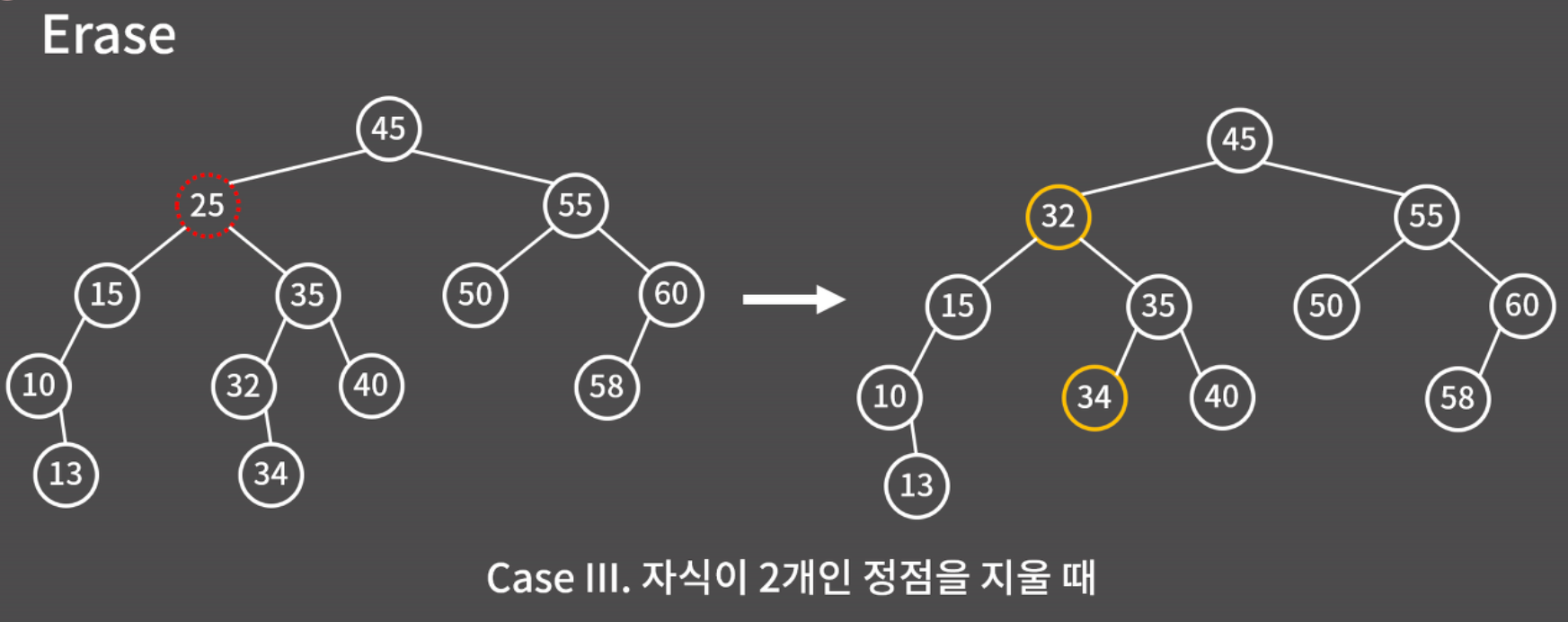
0x02 자가 균형 트리

이진 검색 트리에서 삽입, 검색, 삭제 과정 모두 트리의 높이에 따라 시간복잡도가 정해진다

 

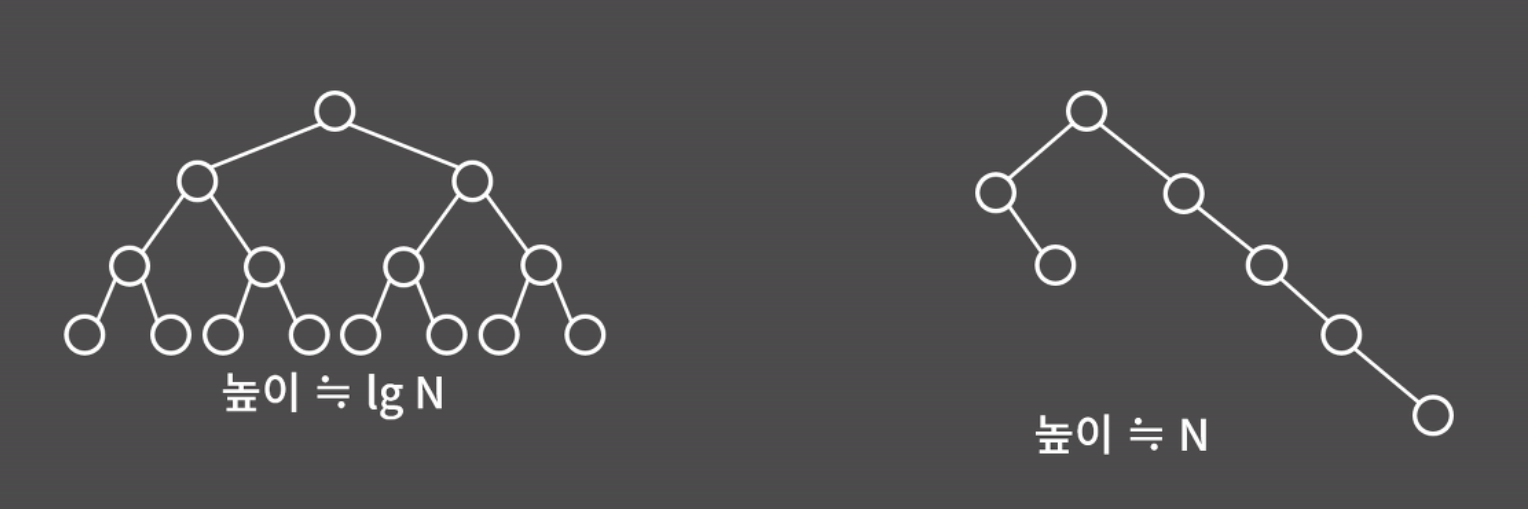
우리는 각 연산을 O(lg N)에 수행하려고 이진 검색 트리를 쓰는건데 만약 트리가 오른쪽 그림처럼 생기면 사실상 Linked List에서 삽입, 검색, 삭제를 한는 것과 별반 차이가 없게된다. 그리고 1,2,3,4, ... 이렇게 크기 순으로 주어진 원소를 삽입한다면 1이 루트이고 나머지 원소들이 오른쪽에 일직선으로 연결되는 편향된 트릐가 되니 이런 트리가 만들어지는 상황은 아주잘 발생할 수 있게된다.

 

 

 

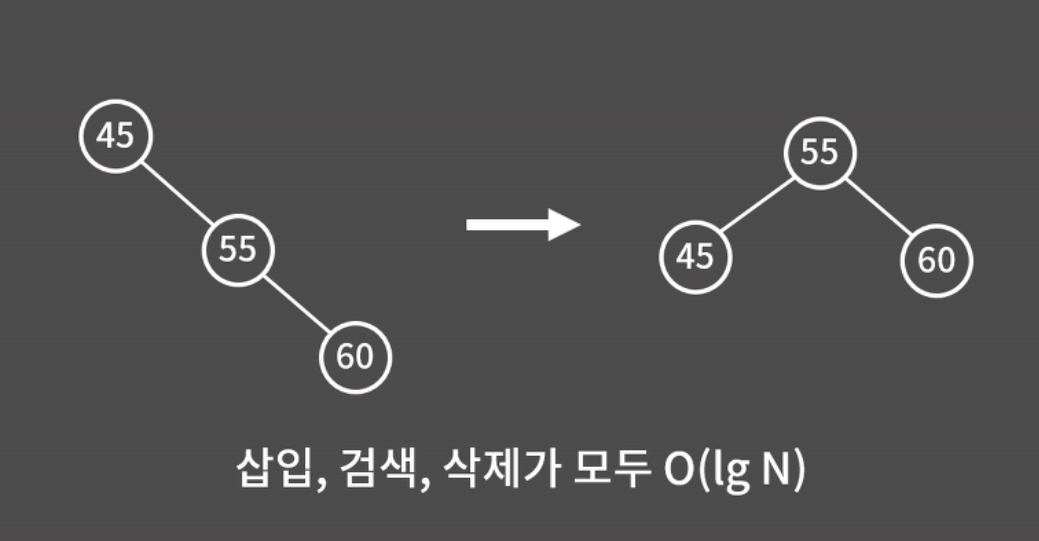
그렇게 때문에 이진 검색 트리가 편향되면 그걸 해결해줄 필요가 있다. 이러한 트리를 자가 균형 트리(Self-Balancing Tree)라고 부르고 대표적으로 AVL 트리, Red Black 트리가 있다. 둘 중에서 AVL은 구현이 조금 쉬운편인데 성능 자체는 Red Black 트리가 더 좋아서 STL에 있는 이진 검색 트리는 Red Black 트리를 가지고 구현되어 있다.

 

원리를 간단하게 설명하자면 위 왼쪽 그림처럼 뭔가 불균형이 발생했을 때 트리를 꺽어버린다. 이렇게 편향성을 해소해주는 자가 균형 트리를 사욜할 때 비로소 이진 검색 트리에서 삽입 검색, 삭제가 모두 O(lgN)이 된다.

 

 

 

0x03 STL

 

 

set에서는 값이 중복되면 안됐는데 multiset은 가능하다, 중복값이 있을때 사용

 

 

 

 

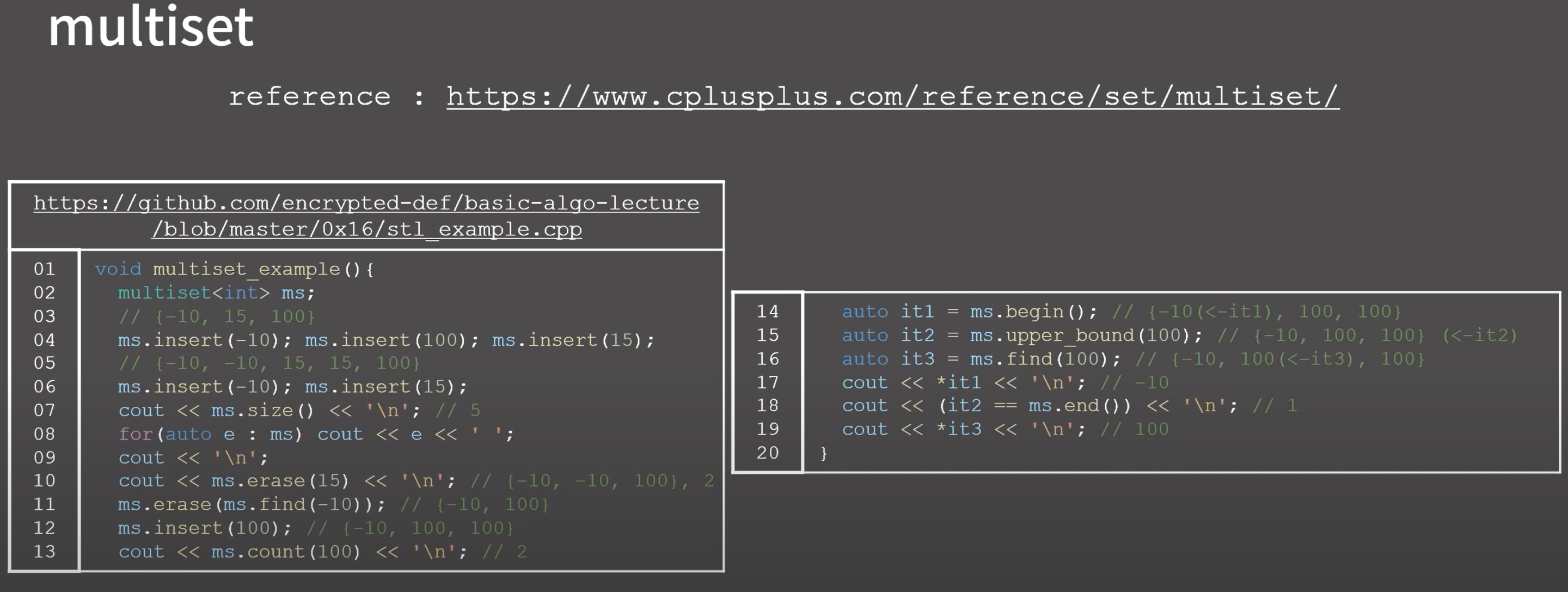
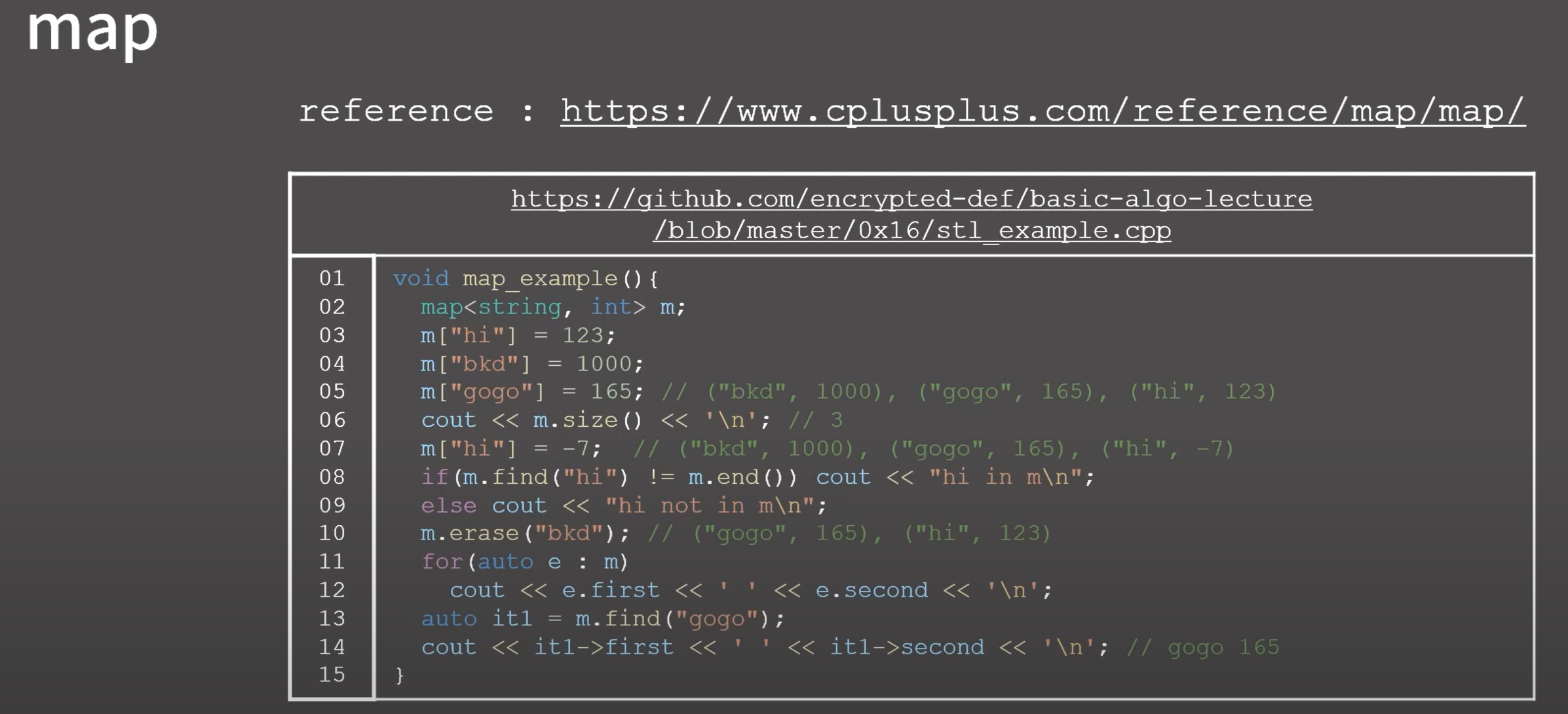
0x04 연습 문제

BOJ 7662번: 이중 우선순위

7662번: 이중 우선순위 큐

 

#include <bits/stdc++.h>
using namespace std;

int main(void){
  ios::sync_with_stdio(0);
  cin.tie(0);
  int t;
  cin >> t;
  while(t--){
    int k;
    cin >> k;
    multiset<int> ms;
    while(k--){
      char com;
      cin >> com;
      if(com == 'D'){
        int q;
        cin >> q;
        if(ms.empty()) continue;
        if(q == 1) ms.erase(prev(ms.end()));
        else ms.erase(ms.begin());
      }
      else{
        int q;
        cin >> q;
        ms.insert(q);
      }
    }
    if(ms.empty()) cout << "EMPTY\n";
    else{
      cout << *prev(ms.end()) << ' ' << *ms.begin() << '\n';
    }
  }
}

 

 

BOJ 1202번: 보석 도둑 

1202번: 보석 도둑

 

#include <bits/stdc++.h>
using namespace std;

#define X first
#define Y second

int n, k;
pair<int, int> jewel[300003]; // {가격, 무게}
multiset<int> bag;

int main() {
  ios::sync_with_stdio(0);
  cin.tie(0);
  cin >> n >> k;

  // 정렬의 편의를 위해 무게/가격을 반대로 입력받음
  for(int i = 0; i < n; i++)
    cin >> jewel[i].Y >> jewel[i].X;
  sort(jewel, jewel+n);

  for(int i = 0; i < k; i++){
    int c;
    cin >> c;
    bag.insert(c);
  }

  long long ans = 0;

  for(int i = n-1; i >= 0; i--){
    int m, v;
    tie(v, m) = jewel[i];
    auto it = bag.lower_bound(m);
    if(it == bag.end()) continue;
    ans += v;
    bag.erase(it);
  }
  cout << ans;
}