[논문 리뷰] High-Resolution Image Synthesis with Latent Diffusion Models

1. 선행 지식

Autoencoder(AE)**와 VAE(Variational Autoencoder) 지식이 필수적인 이유는, LDM의 핵심이 고해상도 이미지 데이터를 직접 다루는 대신, AE/VAE가 만들어낸 저차원 잠재 공간(Latent Space)에서 확산(Diffusion) 과정을 수행하기 때문이다.

Stable Diffusion 이해를 위한 선행 개념: Auto Encoder 및 VAE

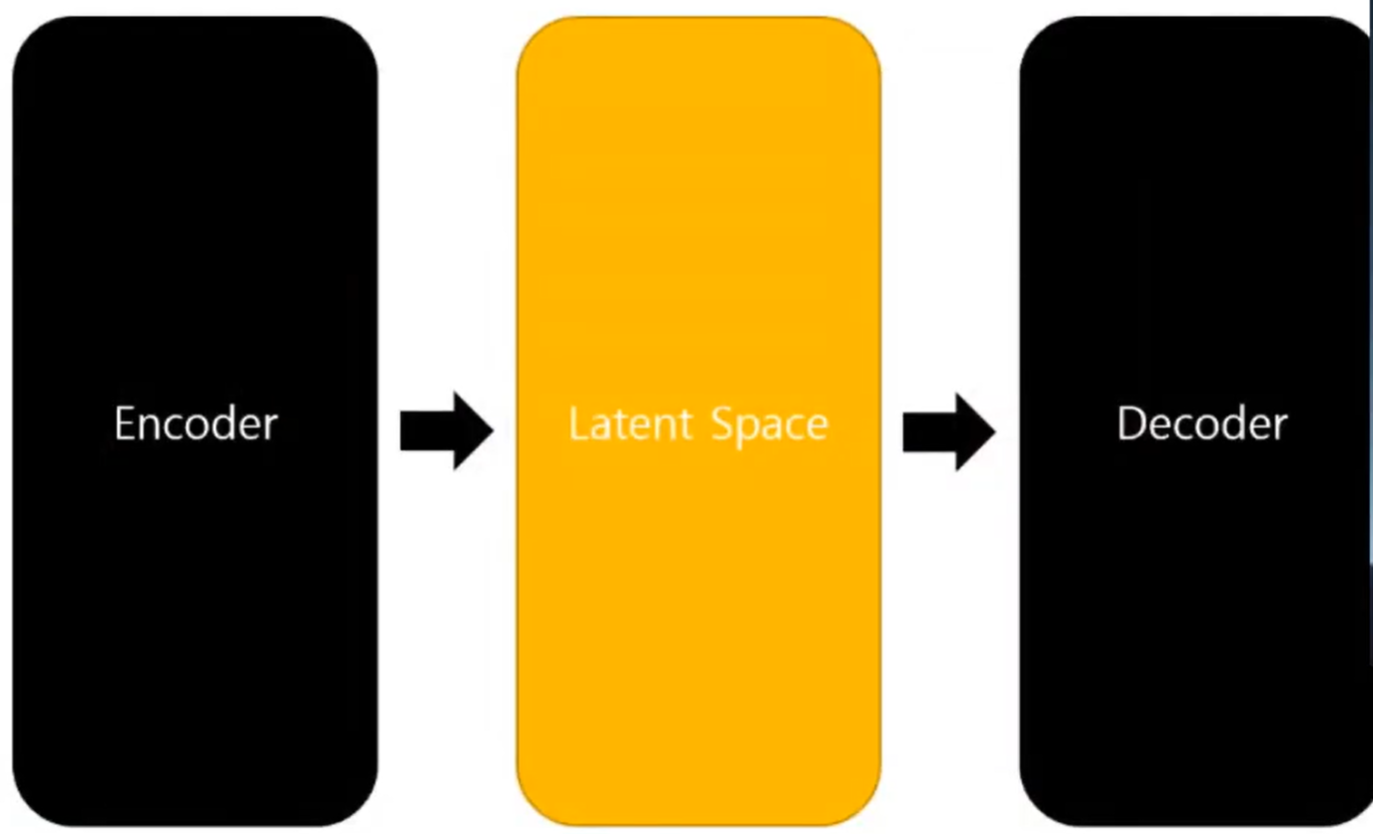
VAE : 이미지와 같은 고차원 데이터를 encoding을 통해서 저차원 공간으로 맵핑을 시킨 다음에 그것을 decoder를 이용해서 생성을 시켜내는 구조.

• Encoder를 이용해서 input을 Latent Space로 맵핑시키는 과정은 PCA 등 성분 분해 개념과 유사
• Latent Space는 의미 있는 정보를 담는 차원 공간
• Latent Variable은 정보를 담는 변수
• Decoder는 이러한 주요 요소들을 다시 복원 시키는 역할

• x 데이터가 너무 고차원 이므로, 이를 다시 작은 분포로 변환(정규부포 변환시 평균과 분산을 이용해서 분포를 표현 가능)
• 샘플링을 하는 과정에서 Reparametrization trick 을 활용해서, 가우시안 분포에서 바로 분포를 추정하는 것이 아닌, noise 값을 더해서 미분가능한 함수로 바꿔준 후에 학습.

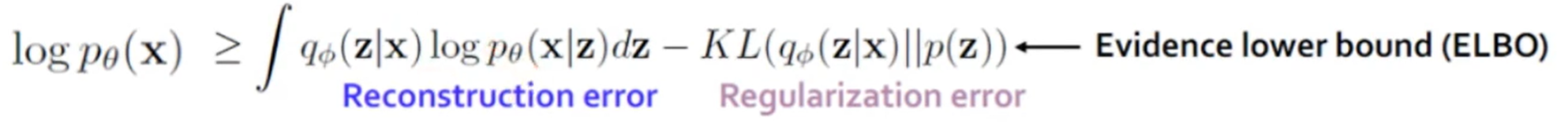
Auto Encoder :

x를 만들어내는 p를 찾아내는는 것. z로 한 번 압축을 한 다음에 이 z를 전제로 했을 때 x를 만들어내는 조건부 확률을 최대화 하는 방식으로 학습.

VAE 손실 함수(Loss) 목표 :

z으로부터 x가 나타날 확률을 최대화 하는 것으로 MLE(Maximum Likelihood Estimation) dl 되며 이는 Cross-Entropy로 표현된다.

Reconstruction Loss: 입력 x가 들어왔을 때 원래대로 잘 복원되는지 측정합니다.

우변의 KL 발산(Kullback-Leibler Divergence) 공식은 이미 잠재 공간을 생성하는 함수(p(z))를 알고 있기 때문에, 두 함수의 분포 차이가 최소 하한(lower bound)이 되도록 하여 정규화 항(regularization term)으로 사용됨.

최소 하한(ELBO)이 되도록 하는 이유우리는 실제 데이터의 확률인 p(x)를 최대화하고 싶지만, 적분 계산이 불가능하기에 대신 ELBO(Evidence Lower Bound)라는 값을 최대화하는 방식을 취한다.

• Evidence (p(x)): 우리가 관찰한 데이터의 확률.
• Lower Bound: p(x)의 실제 값은 알 수 없지만, ELBO보다는 항상 크거나 같다는 것이 수학적으로 증명되어 있다.

따라서 분포 사이의 차이(KL Divergence)를 최소화하면서 ELBO를 최대화하면, 결과적으로 데이터의 확률 p(x)를 간접적으로 최대화하게 됩니다. 이를 통해 모델이 데이터의 복잡한 분포를 효과적으로 학습할 수 있다.

 

 

 

 

 

2. 확산 모델(Diffusion Model)의 기본 원리

2.1 확산 과정(Diffusion Process)과 마르코프 체인

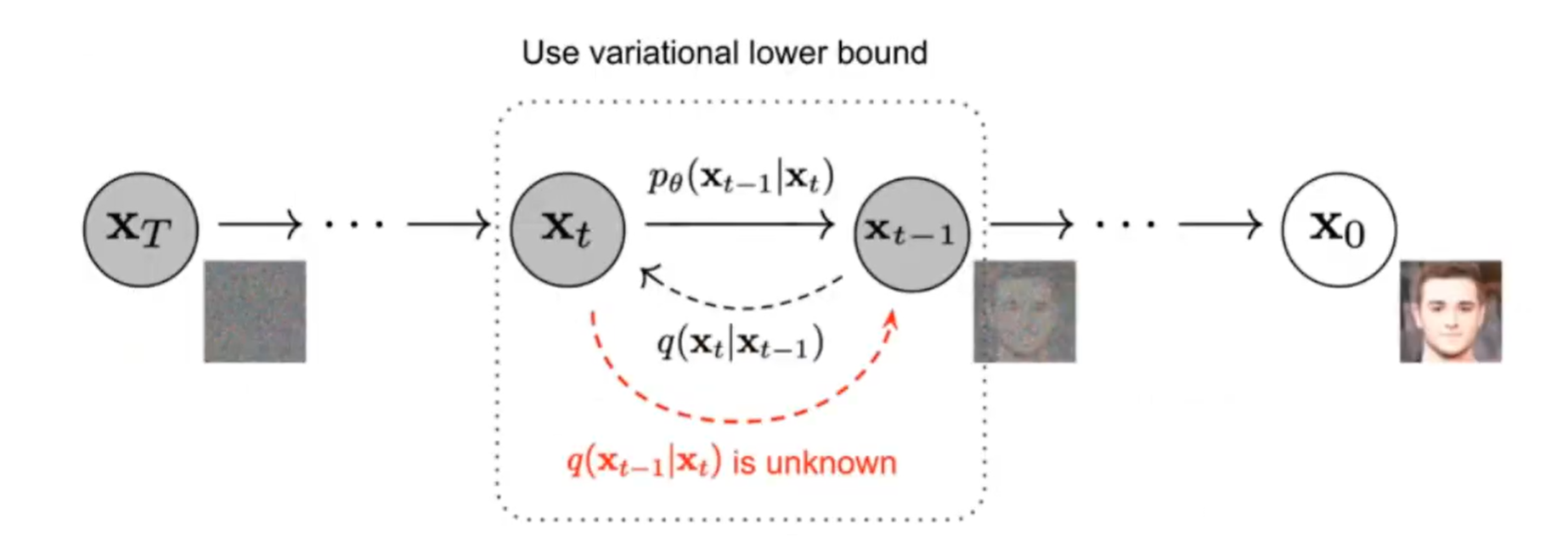
1. 노이즈 주입 방식의 차이:Auto Encoder는 노이즈를 한 번에 주입하는 방식이었다면, 확산 모델은 노이즈를 추가하는 과정 자체를 여러 단계(step)로 분할함
2. 확산 과정: 각 단계가 하나의 함수가 되며, 이 단계를 거칠 때마다 원본 이미지가 가우시안 분포에 가까워지는 과정을 확산 과정이라고 함.
3. 전체 프로세스 정의: 시간 t에서 변화가 가능한 순방향 함수(forward function)를 마르코프 체인(Markov chain) 형태로 구성하는 것이 전체 프로세스의 정의임
4. 마르코프 확산 커널: 이러한 구성을 마르코프 확산 커널(Markov Diffusion kernel)이라고 함
5. beta 파라미터: 이 과정에서 beta라는 파라미터가 사용됨. Step Size B가 매우 작다면 역방향 확산 과정이 Gaussian을 따름.
6. beta_t의 역할: beta_t 파라미터는 t_0부터 t까지의 변환이 얼마나 오래 걸리는지, 그리고 단계(step)가 얼마나 조밀하게 이루어지는지를 결정하는 파라미터임. 성능에 매우 중요한 역할.

Stable Diffusion은 VAE 와 Diffusion models 을 합친 느낌이다.

 

 

 

2.2 LDM( Latent Diffusion Model ) Architecture

1. 구성 요소:
   1. 픽셀 공간에서 인코딩을 통해 잠재 벡터를 추출하는 과정에 확산 프로세스가 적용됨
   2. 추출된 잠재 변수를 디노이징하는 과정(디코더로 전달)이 다시 단계별로 나뉘어지며, 각 단계는 UNet 구조의 함수로 구성됨
   3. UNet은 이미지 분할에 주로 사용되는 특별한 신경망 구조이다. 마치 모래시계처럼 생겼는데, 이미지를 압축했다가 다시 확장하면서 세밀한 부분까지 정확하게 처리할 수 있습니다. Stable Diffusion에서는 이미지의 노이즈를 제거하는 데 사용.
2. 조건화(Conditioning): 텍스트, 이미지 등 다른 도메인 데이터가 입력될 경우, 각 단계에서 어텐션 메커니즘(attention mechanism)을 통해 데이터를 학습함
   1. 크로스 어텐션(Cross-Attention) 이용. 다양한 조건(텍스트, 이미지 등)을 처리하기 위함.
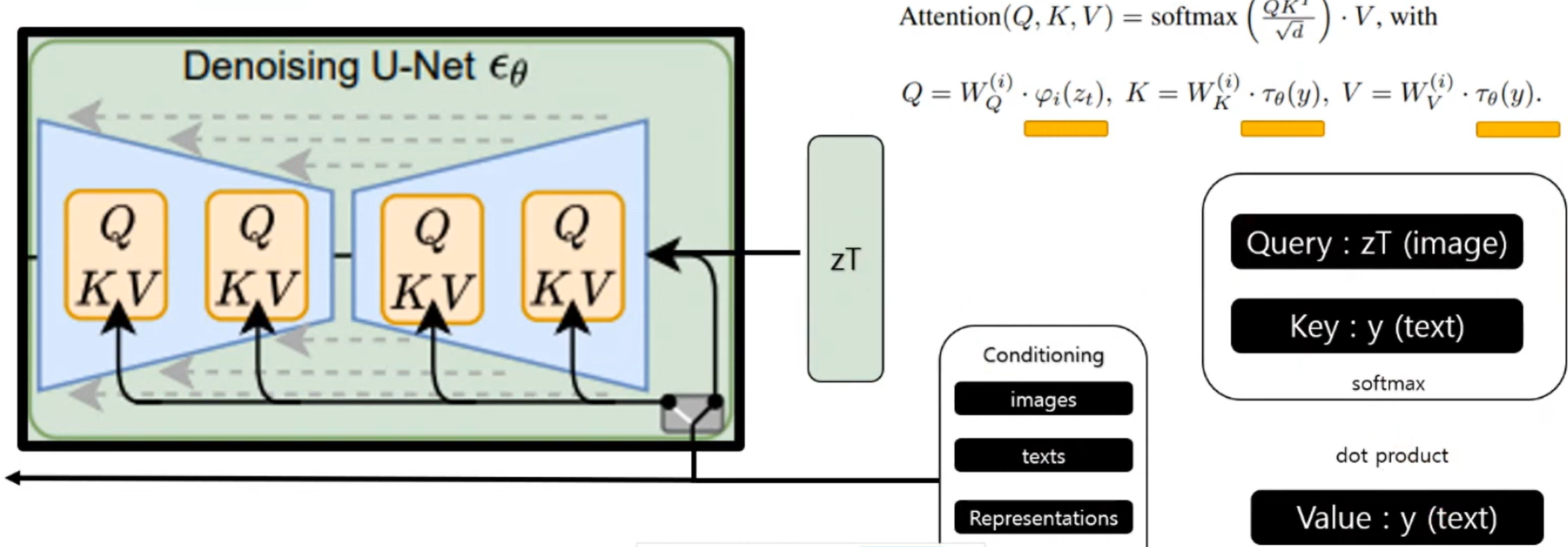
      1. Query (Q): UNet 내부의 중간 특징 맵(이미지 정보)에서 생성됩니다. "이미지의 어느 부분에 어떤 정보를 채워야 할까?"라는 질문 역할
      2. Key (K): 조건 데이터(y)를 전용 인코더(tau_theta)로 처리한 결과물에서 생성됩니다. "내가 가진 조건 정보들 중 어떤 키워드가 있을까?"라는 목록 역할을 합니다.
      3. Value (V): Key와 마찬가지로 조건 데이터에서 생성되며, 실제 이미지에 반영될 세부 정보를 담고 있습니다.

 

 

 

 

 

 

3. Stable Diffusion Model (= LDM)

• 핵심 요약: Stable Diffusion의 핵심은 디노이징 과정에 Auto Encoder를 사용하고, 픽셀 공간이 아닌 잠재 공간(latent space)에서 디노이징을 수행하여 기존 모델들이 요구했던 엄청난 GPU 및 컴퓨팅 비용을 개선한 점임
• 상호 운용성: 크로스 어텐션(cross attention)을 사용하여 서로 다른 도메인의 모델들을 함께 사용할 수 있다는 점이 개선됨
• 논문의 초점: 논문은 기존 확산 모델들이 요구하는 높은 계산 비용을 개선하는 데 초점을 맞춤

3.1 Introduction

기존 모델의 단점: 기존 확산 모델 중 계산량이 많은 모델은 V100 수백 개를 사용하여 며칠 동안 훈련해야 하는 등 학습 및 추론에 필요한 계산 비용이 과도함

이미지 복원 작업(image restoration task)을 수행했을 때의 결과

이 비교에서는 FID(Fréchet Inception Distance) 지표를 사용. FID 지표는 생성이미지와 실제 이미지의 유사도 측정 값. 낮을수록 좋은 지표로 해석할 수 있음. 이미지 크기를 크게 줄이는 공격적인 다운 샘플링(less aggressive downsampling)을 하지 않고도 효율적으로 작업을 수행했음을 강조한다.

 

 

 

 

3.2 Method

학습 순서: 이 논문에서는 Auto Encoder를 먼저 학습시킨 후, Auto Encoder와 전체 프로세스를 함께 학습시킴

구조적 정의: UNet 아키텍처를 Auto Encoder 외에 매 단계 학습시키는 구조를 갖춘다고 볼 수 있음. 이러한 구조를 잠재 공간에서 학습하는 확산 모델, 즉 잠재 확산 모델(Latent Diffusion Model)로 정의

인코더의 재활용성: 이전에 사용된 인코더는 전이 학습(Transfer learning)처럼 다른 여러 작업에 반복적으로 사용될 수 있음

실험 증거: 논문 뒤편의 부록을 보면, 다양한 작업에 해당 인코더를 사용하여 빠른 속도로 실험을 할 수 있었음을 확인할 수 있음

다양한 작업으로는 비조건부 이미지 합성(unconditional image synthesis), 즉 이미지 복원 작업임. 세부적으로는 인페인팅(Inpainting)과 슈퍼 해상도(Super resolution) 이다. 이러한 작업에서 계산 비용이 대폭 감소함. 노이즈 이미지와 함께 cross attention이 사용됨.

 

 

 

Denoising U-Net

 

노이즈 주입 과정(injecting noise) 자체에는 신경망을 거의 사용하지 않음. 노이즈 주입 과정은 학습할 필요가 없으며, 고정된 함수를 사용. 따라서 원본 확산 모델 자체는 신경망을 사용하지 않으며, 노이즈 주입은 미리 정해진 함수에 따라 이루어짐

단계 수의 영향은 논문에서는 단계 수가 많을수록 좋다고 표현했지만 최적의 단계 수를 찾는 것이 중요함

 

LDM은 이미지 생성 과정을 지각적 압축(Perceptual Compression)과 의미적 압축(Semantic Compression)이라는 두 단계로 나눕니다. LDM은 오토인코더를 통해 불필요한 고주파 디테일이 제거된 '잠재 공간'에서 작동하므로, 실제 이미지의 핵심적인 의미와 개념적 구성(Semantic bits)에만 집중할 수 있습니다.

 

논문에서는 LDM의 신경망 뼈대로 UNet 구조를 사용하는 이유가 이미지 데이터에 최적화된 귀납적 편향을 제공하기 때문이라고 설명합니다. 귀납적 편향(Inductive Bias)은 모델이 학습하지 않은 데이터에 대해서도 올바른 예측을 할 수 있도록, 모델의 구조 자체가 특정 데이터의 성질(여기서는 이미지의 공간적 구조)을 잘 이해하도록 설계되어 있는 것을 말합니다. Unet은 2D 컨볼루션 레이어(Convolutional layers)를 기본으로 합니다. 컨볼루션 연산은 이미지의 인접한 픽셀 간의 관계를 파악하는 데 매우 효과적이며, 이는 이미지와 같은 공간적 데이터를 처리하는 데 최적화된 귀납적 편향을 제공합니다. 이는 다른 생성 모델(예: 순수 트랜스포머 기반 모델)이 데이터를 과도하게 압축해야만 했던 한계를 극복하게 해주며, 비교적 약한 압축만으로도 고품질의 이미지를 재구성할 수 있게 합니다. UNet 특유의 스킵 커넥션(skip connection)은 저수준의 공간 정보와 고수준의 의미 정보를 효과적으로 결합하여, 복잡한 이미지를 생성할 때 세밀한 부분까지 놓치지 않도록 돕는다.

 

 

Cross-Attention Mechanism

 

zT (노이즈가 오염된 이미지)는 쿼리 값(query value)으로 입력됨.

입력으로 넣고자 하는 텍스트는 임베딩(embedding)되어 키 값(key value)으로 사용됨.

두 가중치를 내적(dot product) 후, 소프트맥스(softmax) 값으로 가중치를 추출하고 다시 텍스트 이미지로 내적하여 사용함.

 

 

 

손실 함수

 

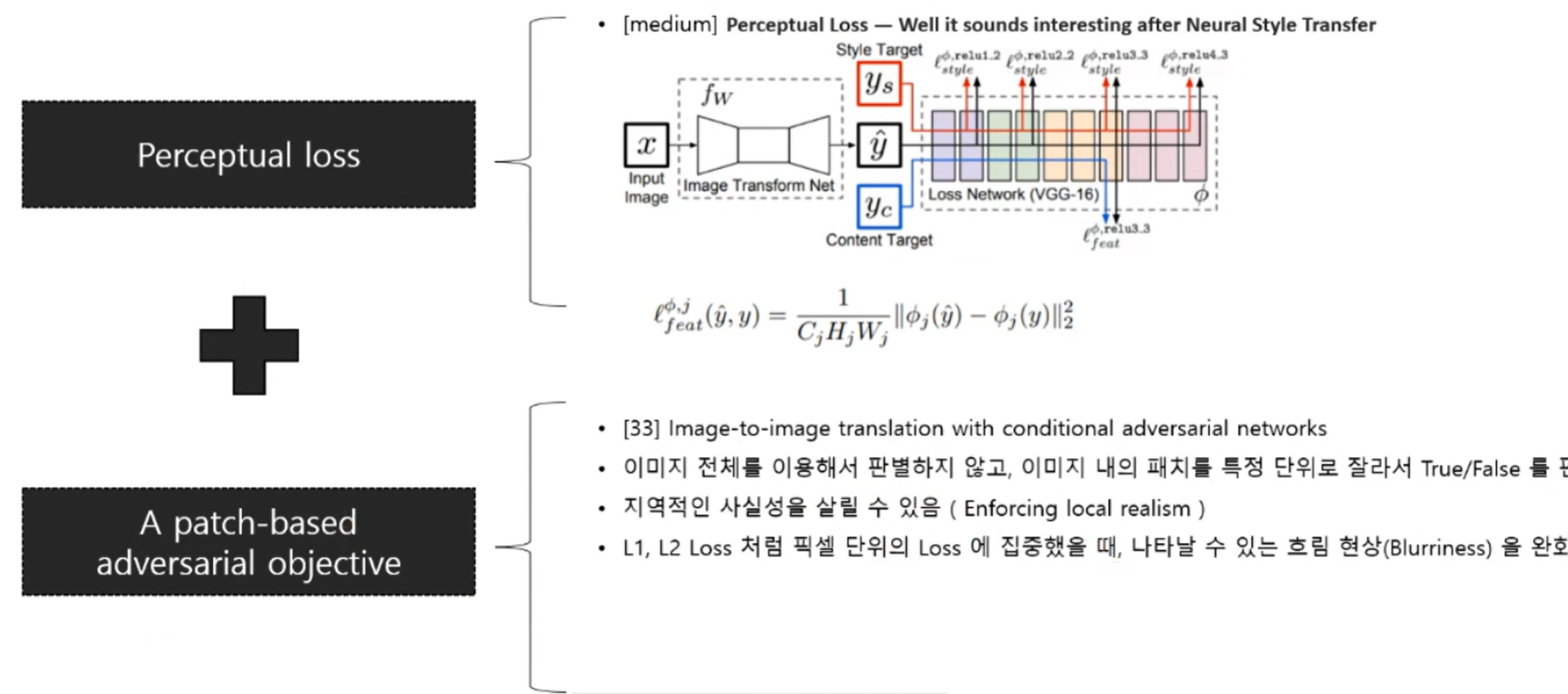
지각 손실(Perceptual loss)과 패치 기반 적대적 목적 함수(patch based adversarial objective)를 사용

1. 지각 손실: 네트워크상의 특징 맵(feature map)을 추출하여 각 특징 맵에 대한 거리를 계산함
2. 패치 기반 적대적 목적 함수:
   1. 전체 이미지가 맞는지 틀리는지에 대한 점수를 측정하는 대신, 패치 단위로 True/False를 판별하는 방식임
   2. 이 방식을 사용함으로써 국소적 사실성(local realism)을 보존할 수 있으며, L1 또는 L2 손실 사용 시 발생할 수 있는 흐림 현상(blurriness phenomenon)이 많이 완화됨

 

 

 

3.3 Experiments

 

Evalution metrics for unconditional image synthesis

 

복원 테스트에서 256 x 256 기준 FID 기반으로 SOTA(State-of-the-Art)를 달성했다고 함

 

 

 

Evaluation of text-conditional image synthesis

 

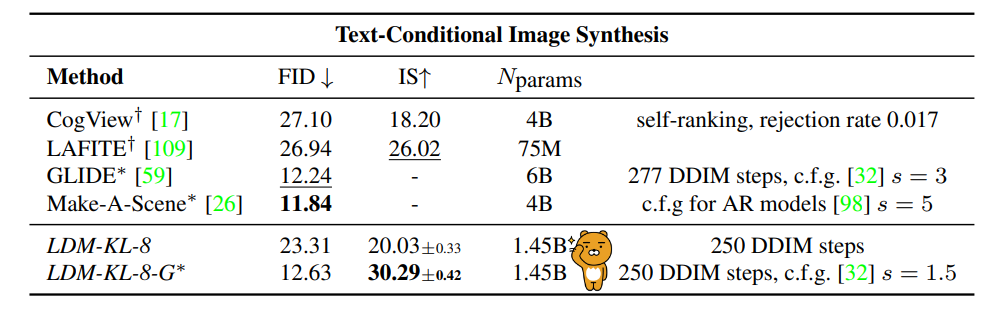
Text to Image 합성에 대해서는 FID상으로도 준수한 점수를 보여주고 있는데, 중요한 것은 60억개 달하는 params를 10억개로 크게 줄였다는 것을 강조한다.